Spitzwinkliges Dreieck

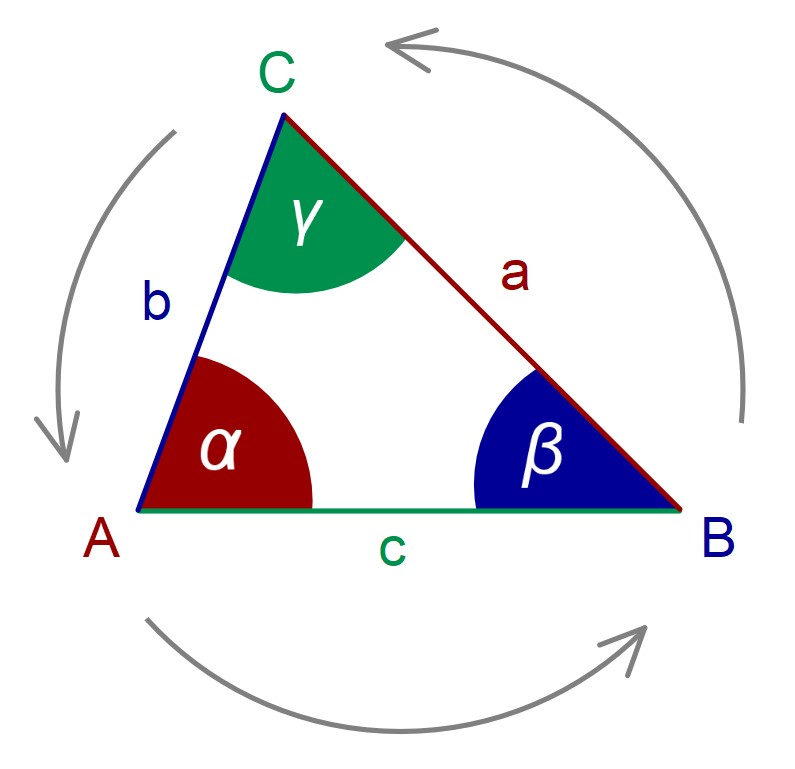
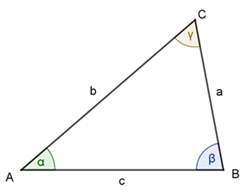
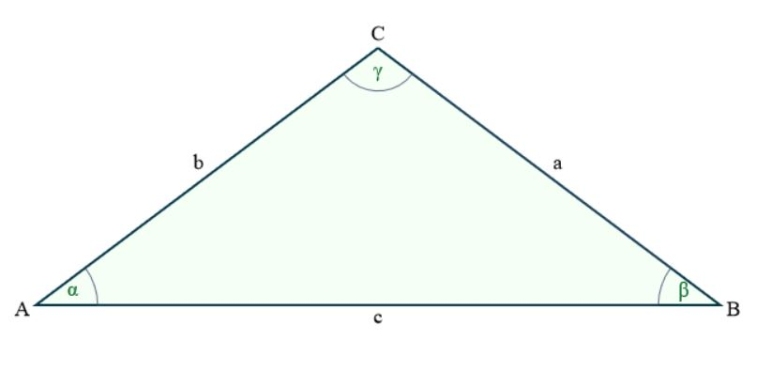
Ein spitzwinkliges Dreieck ist ein Dreieck, bei dem alle Winkel kleiner als 90° sind. Die drei Seiten müssen nicht unterschiedlich lang sein.

Ausgezeichnete Punkte

Im spitzwinkligen Dreieck liegen die vier „klassischen“ ausgezeichneten Punkte, Umkreismittelpunkt ${\displaystyle U}$ (hellgrün), Schwerpunkt ${\displaystyle S}$ (dunkelblau), Inkreismittelpunkt ${\displaystyle I}$ (rot) und der Höhenschnittpunkt ${\displaystyle H}$ (hellbraun) sowie auch der Mittelpunkt ${\displaystyle F}$ des Feuerbachkreises (beides hellblau), innerhalb des Dreiecks.

Auf dem Feuerbachkreis liegen dessen neun ausgezeichnete Punkte. Im Bild sind dies die Seitenmittelpunkte ${\displaystyle J,M}$ und ${\displaystyle O,}$ die Mittelpunkte der sogenannten oberen Höhenabschnitte ${\displaystyle E,K}$ und ${\displaystyle N}$ sowie die Höhenfußpunkte ${\displaystyle D,G}$ und ${\displaystyle L.}$

Die Punkte ${\displaystyle U}$, ${\displaystyle S}$, ${\displaystyle F}$ und ${\displaystyle H}$ liegen dabei, wie bei allen Dreiecken, auf der Eulerschen Gerade ${\displaystyle e}$ (rot).

Siehe auch

• Dreieck
• Gleichseitiges Dreieck
• Gleichschenkliges Dreieck
• Rechtwinkliges Dreieck
• Stumpfwinkliges Dreieck
• Ausgezeichnete Punkte im Dreieck

Weblinks

• Eric W. Weisstein: Acute Triangle. In: MathWorld (englisch).

Einzelnachweise